Lagrange Points

(for a derivation, see Worlds Apart, pp229-234, or Intro to Modern Astrophysics, section 17.1)

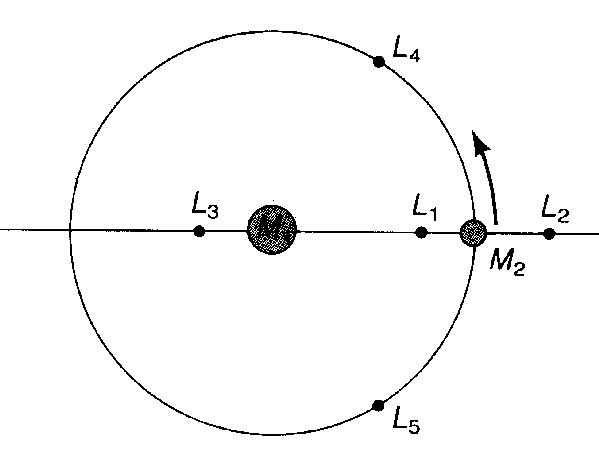
Consider two bodies orbiting one another. In a rotating frame of reference, the total force at any point is the sum of the gravitational force from the two bodies plus the centrifugal force of the rotating system.

It can be shown that there are certain points where the net force acting on an object is zero. These points are called the Lagrange Points.

Objects at these point do not orbit either body individually, but stay fixed relative to both bodies (although, of course, the whole system is in motion).

It can also be shown that:

L1, L2, and L3 are not truly stable -- if an object sitting at these points was perturbed, it would drift away from the Lagrange point.
L4 and L5 are stable, as long as the mass ratio (M1/M2) < 0.0385.

For example, the Sun-Jupiter system. Mjup/Msun = 0.001, so L4 and L5 should be stable. In fact, we find Jupiter's Trojan asteroids there.

What about Earth-Moon? Mmoon/Mearth = 0.012, so again L4 and L5 should be stable.

However, we don't find any Earth Trojan asteroids -- perhaps L4 and L5 are not stable after all. Why might these points be unstable in the Earth-Moon system?