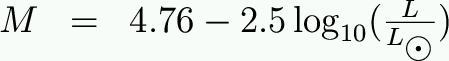Magnitudes and the Inverse Square Law 

Go back to the concept of radiant flux, and remember that light follows an inverse square law. In other words, if you move a light bulb twice as far away, it appears four times fainter. Mathematically we can relate flux (f in erg/s/cm2) to luminosity (L in erg/s) by

So, not surprisingly, a star's apparent brightness depends on both its luminosity and its distance.

A star's observed magnitude is called its apparent magnitude (m), since is not a true measure of a fundamental property of the star.

Let's look at something which is a fundamental property of the star - its true brightness. We will define this as the brightness the star would have if it were 10 parsecs away from us. On the magnitude scale, we call this the star's absolute magnitude (M). How do we do this?

Start by defining f10 to be the flux you would receive from the star if it were 10 parsecs away. We can then relate distance (d) to absolute and apparent magnitude like this:

or
So we have an equation which relates three items: m, M, and d. If we know two, we can calculate the third.

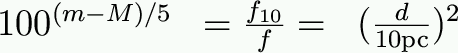
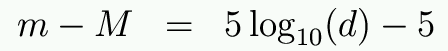
Often if we know what kind of star it is, we can estimate its luminosity (and, thus, M). We can then measure its apparent magnitude (m) and solve for distance. Since m-M is a measure of distance, it is called the distance modulus.

Question: what is the absolute magnitude of the Sun? Answer: M=4.76

(this, technically, is the bolometric absolute magnitue of the Sun -- more on that later)

We can use this in a nifty way to relate absolute magnitude to solar luminosity. Remember our definition of magnitude:

If both stars are the same distance, the ratio of their fluxes is the same as the ratio of their luminosities. If we make this distance 10 pc, then the m's become M's. Then let's make star #2 the Sun. Doing all this, we get: