Overcoming the Coulomb Barrier

Remember the problem with fusing hydrogen nuclei -- the coulomb barrier

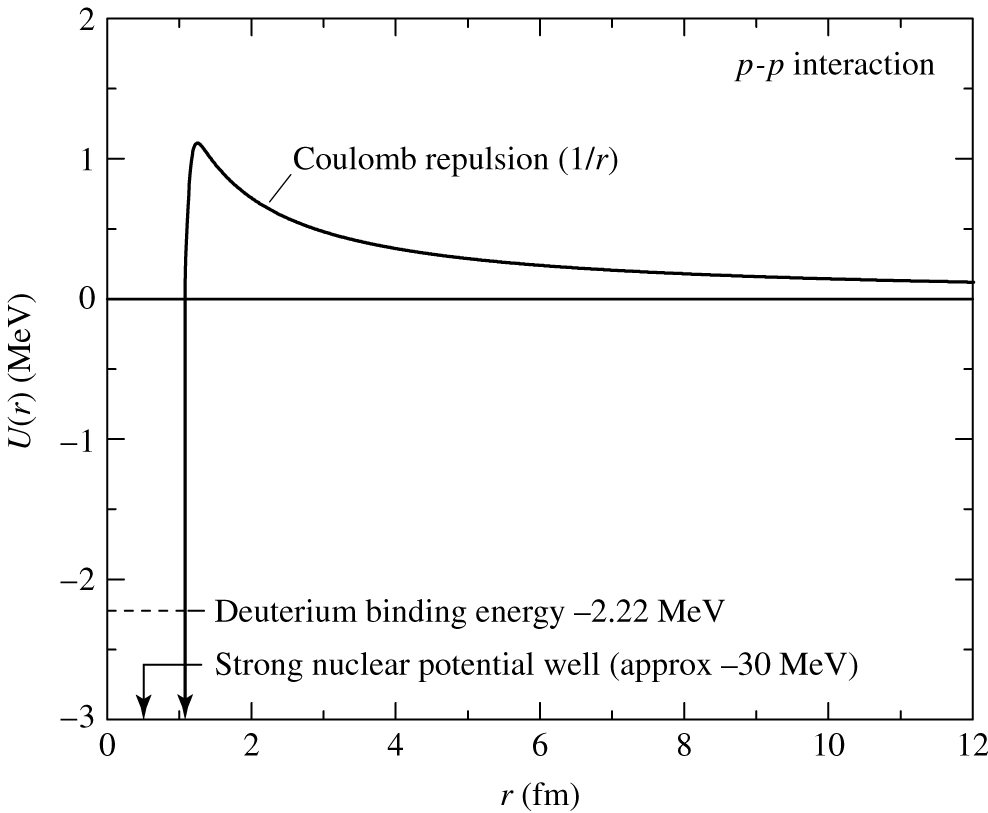
Protons have positive charge. Like charges repel -- the electromagnetic force.
We need to overcome this repulsion to have the nuclei fuse.

How do we do this? Energetic nuclei! How do we make energetic nuclei?

The Maxwell-Boltzmann Distribution

Particles at a given temperature will have a distribution of speeds (and therefore a distribution in energies):

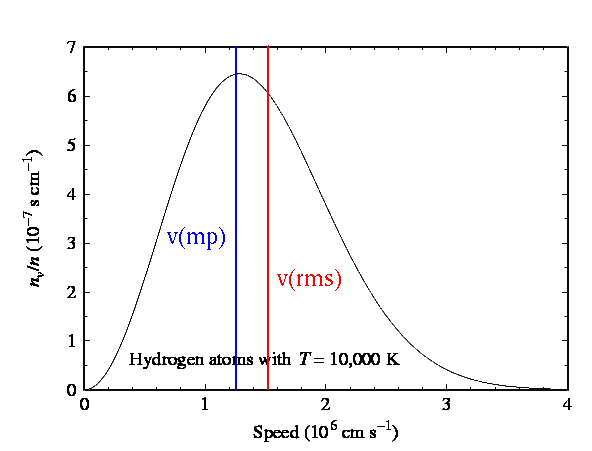
This is a probability distribution. The probability of a particle having a given energy E is

And, in this distribution, particles have a most probable velocity and an average velocity:

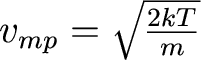
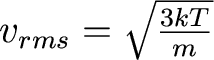
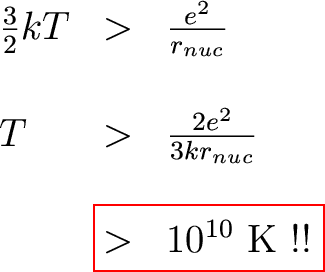
So to overcome the Coulomb barrier, particles must have sufficient (thermal) kinetic energy to exceed the Coulomb repulsion. Let's see:

Whoops.

Well, things aren't that bad. There is a high energy tail to the distribution. But this alone isn't enough. We need to look to quantum mechanics.

Quantum Mechanical Tunneling about as close as you can get to magic...

The Heisenberg Uncertainty Principle: It is not possible to know both a particle's momentum and position to unlimited accuracy. In other words,

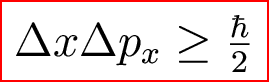
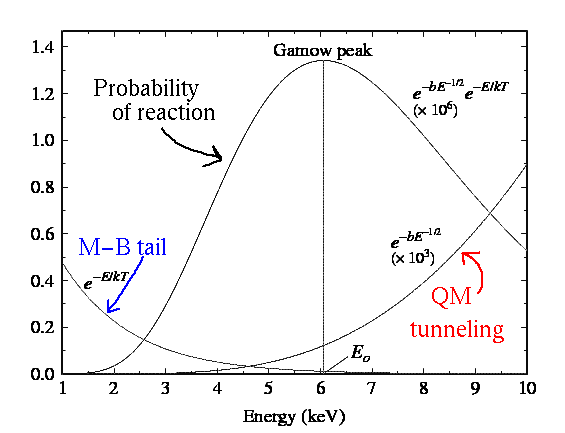
So a particle of a given (insufficient) energy just might find itself inside the nucleus even though classical mechanics say it has no business being there. Wow...

So combining the high energy tail of the M-B distribution and the possibility of QM tunneling (which rises as energy rises), we get the Gamov peak:

So particles with 3-10 keV of energy (which there are plenty of in the Sun's core) can overcome the Coulomb barrier.

Voila! Nuclear Reactions!