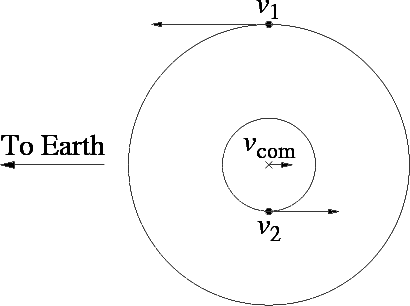
Spectroscopic Eclipsing Binaries

Many times the stars are too close -- or one star is too bright -- for us to actually see two stars. Yet by looking at the spectrum of the star we can tell it is a binary, and derive the orbit and mass of the stars. These are spectroscopic binaries.

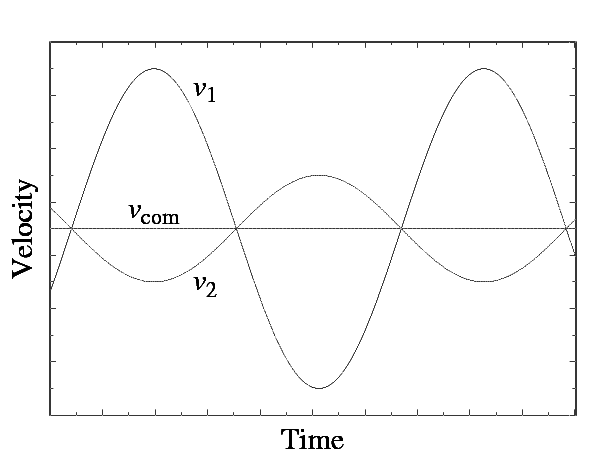
How? Watch the absorption lines in the star. They will shift in wavelength due to the doppler shift as the stars orbit each other. Turn those shifts into velocities and you can construct the velocity curve of the binary:

Note that the orbit need not be circular, in which case the velocity profiles are not sinusoidal:

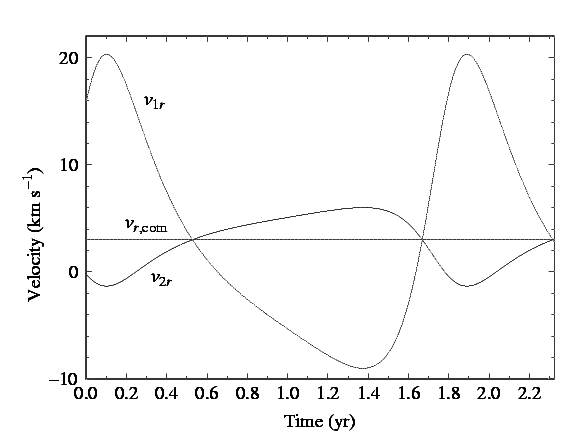
How do we use this to derive properties of the stars?

Remember how we define the center of mass in an orbital system:

M₁r₁ = M₂r₂

where r₁ and r₂ are the distances of each object from the center of mass.

We can do the same thing here with the center of mass velocity:

Now, how do we get the sum of the masses? Note that velocity, period, and semimajor axis are related:

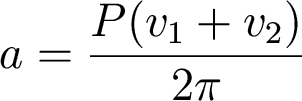
We can plug this expression for a back into Kepler's third law and solve for the mass sum:

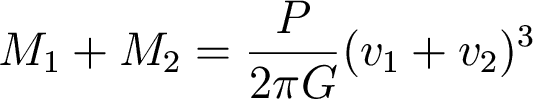
Here we have the sum of the masses and the mass ratio, so we can solve for the individual masses as well. Cool!

Why isn't life this easy?

Again, there is no reason why nature would oblige us by putting the orbit plane right along our line of sight. It is usually inclined:

We would like i=90. But that's not usually so.

In this case, we don't measure true v, we measure observed v_o = v*sin(i). This complicates the analysis:

There is one very neat class of spectroscopic binary called eclipsing spectroscopic binaries.

These are binaries which actually pass in front of another (from our line of sight) so that we get periodic eclipses. The star Algol is an eclipsing binary:

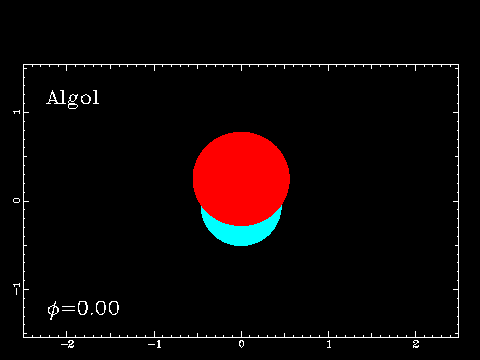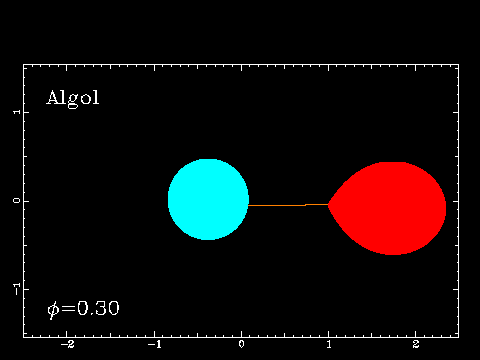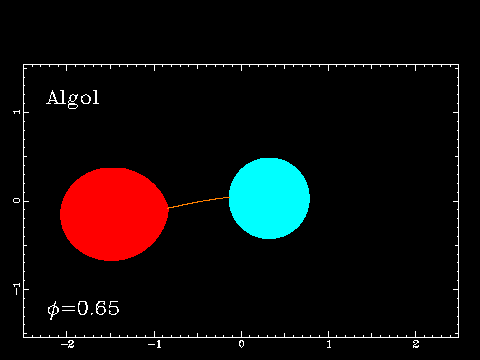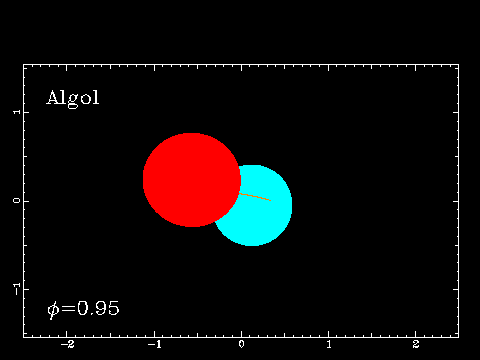
This animation courtesy Robert Mutel, University of Iowa

Algol's brightness varies quite a bit. Normally it has a magnitude m=2.1, but fades to m=3.4 during minimum. The eclipse lasts 10 hours, and occurs every 2.87 days. Algol is sometimes referred to as the Demon Star.

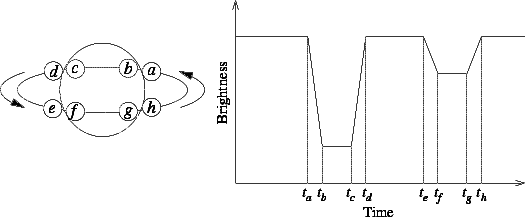
In this case, what is the inclination angle of the orbit?

By combining the light curve and the velocity curve, we can also get the radii of both stars. How?

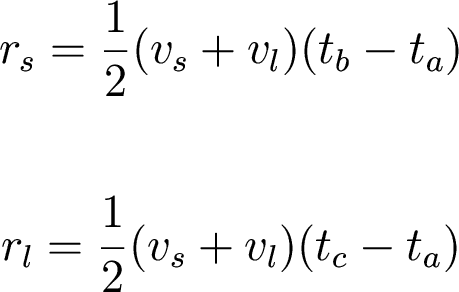
From the brightnesses and colors of the star during the two eclipses, we can also get information on the ratio of the temperatures of the stars (how?).