Structure and Stellar Populations of Elliptical Galaxies
Note: we will
almost exclusively be talking about normal ellipticals. Dwarf
ellipticals (dE's) and dwarf spheroidals (dSph's) are different animals
entirely...
| Elliptical galaxies are generally
smooth and
relatively featureless spheroidal galaxies.
Like the bulges of (some) spirals, ellipticals
are often characterized by a
surface brightnesses profile which follow the de Vaucouleur or
r-to-the-quarter
law: log(I) ~ r1/4
Are ellipticals and spiral bulges the same
thing?
No! The similarity ends there...
But using this luminosity profile, we can
characterize the effective radius
(re) as
the radius containing half the total light of the galaxy, and the mean surface brightness of the galaxy
inside
that radius (<Ie>). One measures the size of the
galaxy,
the other measures the luminosity density.
(Note that <Ie> measures in linear units (Lsun/pc2, for example), while <mue> measures in surface brightness units (mags/arcsec2). Either way, they measure the same thing.)
|
 |
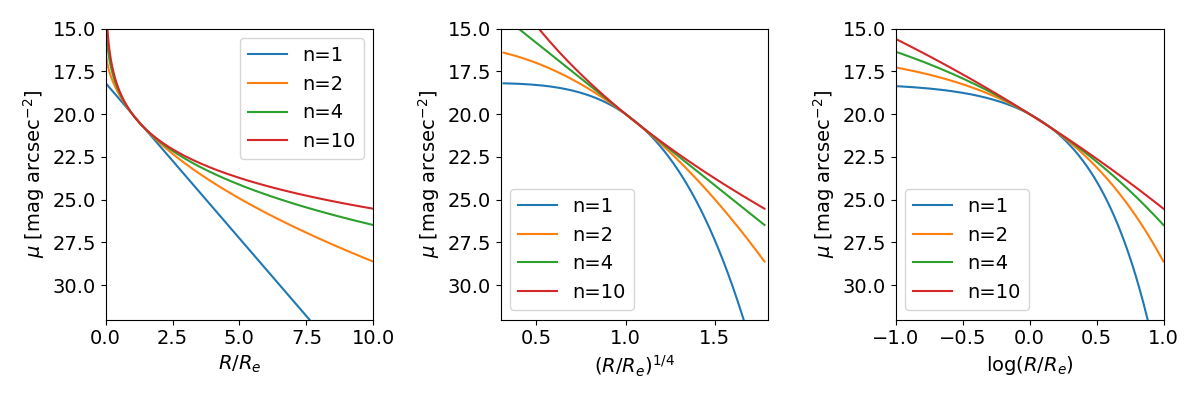
In detail, though ellipticals are found to have
diverse surface brightness profiles, and people often use a more
generalized Sersic
profile to describe galaxies. This mathematical
profile is log(I)
~ r1/n,
and is characterized by re, <Ie>, and a Sersic index
n. If we plot surface brightness (mu, in mags/arcsec2) versus radius, it looks like this:
Note: n=1 would be an exponential, while n=4 is the classical r-to-the-quarter law
For example, the massive galaxy at the center
of the Virgo cluster (M87, a "cD galaxy") has a very extended n ~ 10-11
profile. Inner regions show rapid dropoff in surface brightness, outer
regions fall off much more slowly, showing an extended faint halo of
light (from Janowiecki et al 2010):

Stellar populations
We've seen that elliptical galaxies are much redder than spiral
galaxies. They also typically have much less neutral hydrogen gas. What
does this suggest about their star forming histories?
Population Synthesis reminder
Stellar population
synthesis
tracks: B-V color vs age, for an evolving "single burst" population of stars with different metallicities:
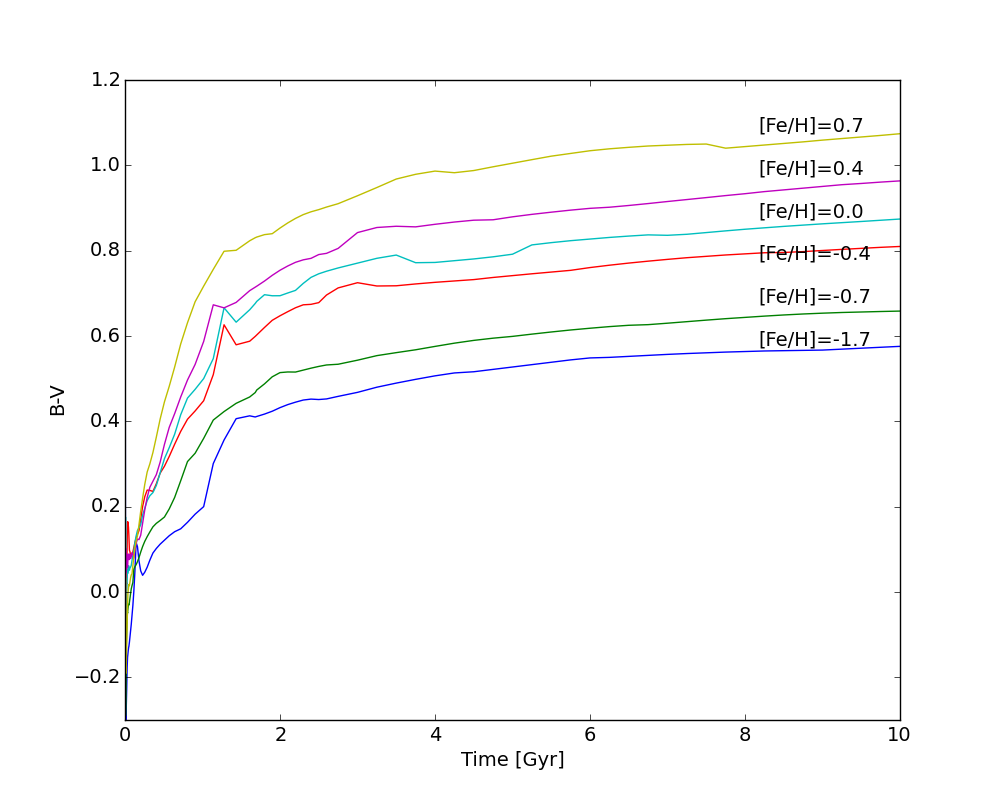
So two things make a stellar population red: old
age, and high metallicity.
The colors of a galaxy cannot distinguish between the two.
Review question: why would high metallicity
make
stars redder?
Elliptical galaxies (like spirals) show a color-luminosity
relationship: brighter, more massive galaxies
are
redder. In elliptical galaxies, this is well-established to be a metallicity effect,
not age. So brighter galaxies are more metal-rich.
The differences between elliptical galaxies and star
forming spirals can be seen in plots of color versus luminosity or stellar mass:
they form a distinct "red sequence" which is offset from the "blue
cloud" of star forming galaxies:
Remember terminology: "early-type" means E/S0, "late-type" means Sb/Sc/Irr.
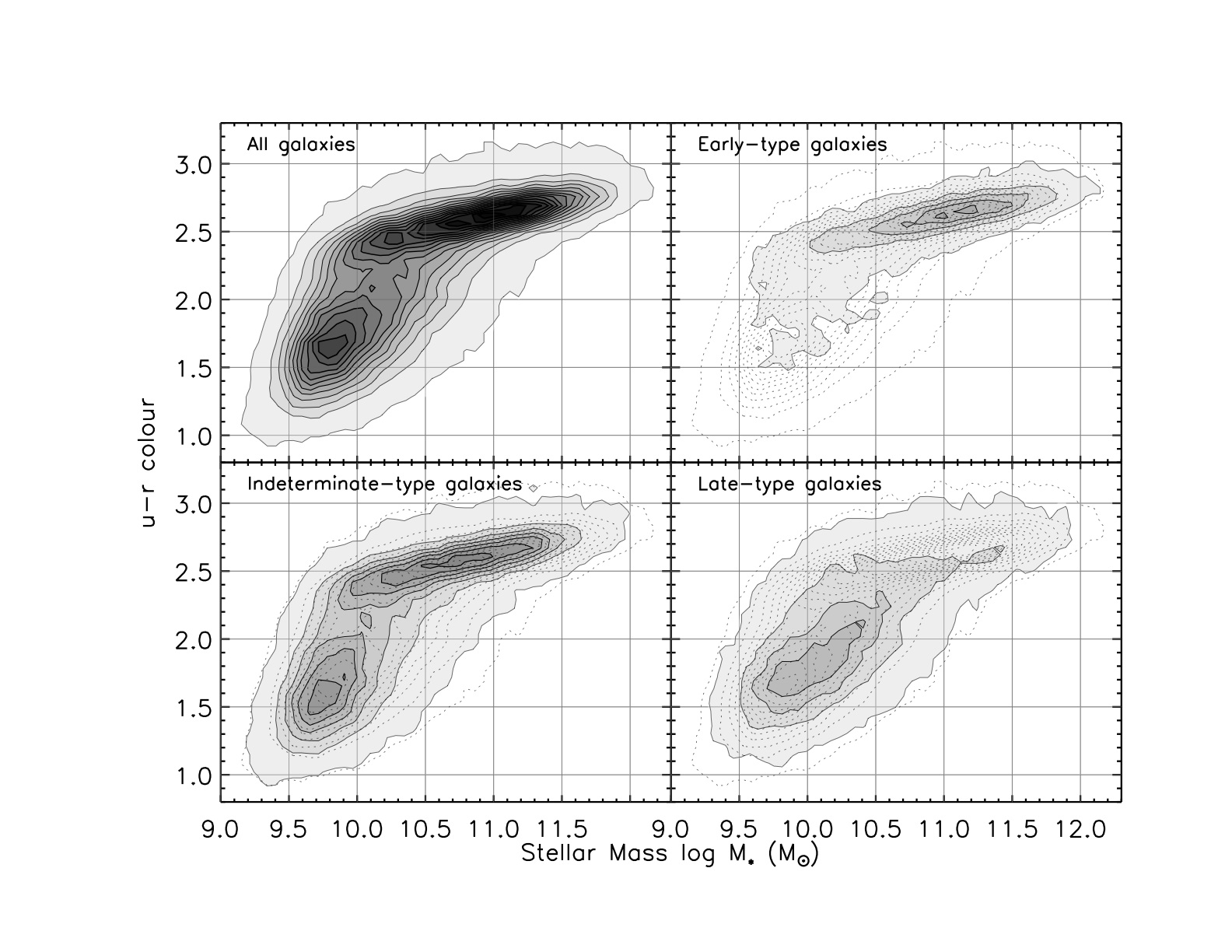
(from SDSS data, courtesy Kevin Schawinski)
Gas content
Actually ellipticals are not devoid of gas -- it's just not
neutral hydrogen, or molecular gas. So what is it?
Look at the elliptical galaxy M49 in optical and
X-ray:

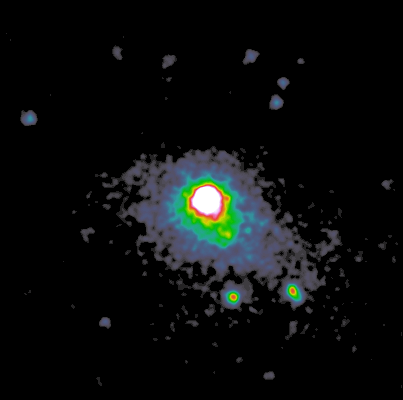
(Thanks to Beth Brown, University of Michigan)
There is extended, X-ray emitting gas. How hot would
it
have to be to emit X-rays? Set the energy of an X-ray photon equal to
the
thermal energy of particles:
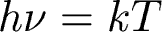
Solving for T, we get a temperature of ~ 106
K
or so.
Mass estimates range from 108 to maybe as
much
as 109 Msun of hot gas in ellipticals. The metallicity of this gas is low, but not super low -- it's ~ 1/3 solar.
Questions to consider:
- Where did this gas come from?
- Why is it hot?
- What holds it up?
Also, some galaxies do have neutral hydrogen -- check out the nearby elliptical galaxy Centaurus A (Schiminovich et al 1994):
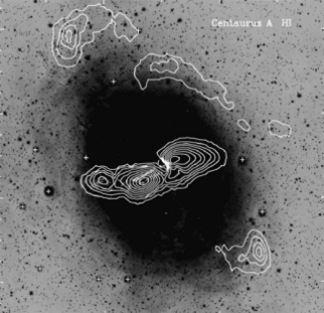 optical starlight in greyscale
HI 21-cm emission in contours
optical starlight in greyscale
HI 21-cm emission in contours