Moving Cluster Parallaxes

Remember what the space motion of a star looks like:

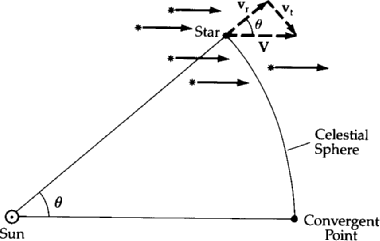
the total space velocity V can be broken into the radial velocity (v_r) and the tangential velocity (v_t)

The radial velocity we get via its doppler shift.
To get the tangential velocity we need its proper motion and distance:

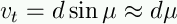
which would be in units of pc/yr if d was in pc and mu in radians/yr.

We can convert this to more familiar units:

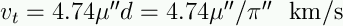
where pi is parallax in arcsec and mu is proper motion in arcsec/yr.

So if we know proper motion and distance, we can solve for tangential velocity. Alternatively, if we knew tangential velocity and proper motion, we could solve for distance. That's the key to the moving cluster parallax. Watch this...

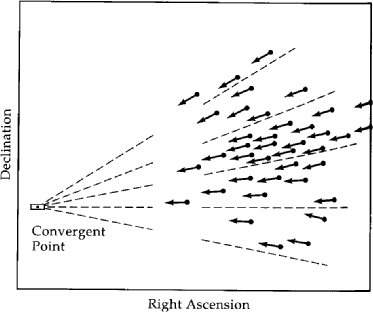
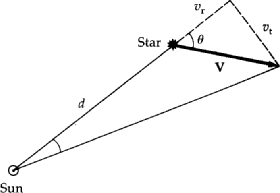
Think of a cluster of stars moving through space. Their proper motion will appear to converge towards a certain point in space called the convergence point:

from geometry, we know that

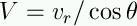so that

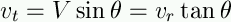Equating our two expressions for v_t we get

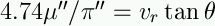or

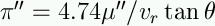So if we measure the proper motion, radial velocity, and convergence point distance, we get the "parallax" -- or really the distance -- to the cluster.

Question: Why is it helpful to get the distance to a star cluster rather than to a bunch of individual stars scattered randomly in space?

from geometry, we know that
so that
Equating our two expressions for v_t we get
or