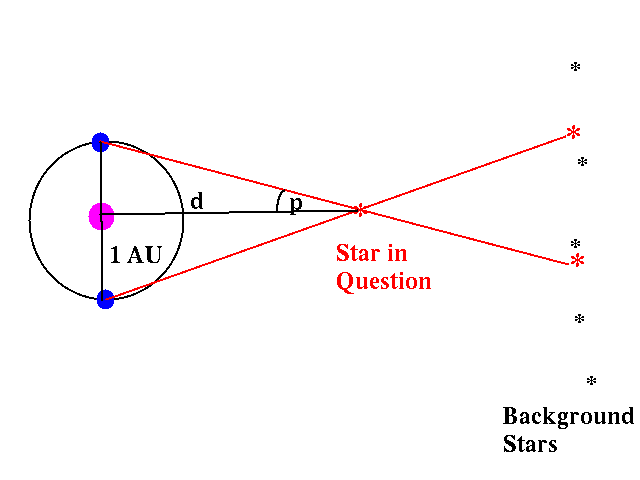
Okay, so let's do this with stars.
Instead of closing one eye and then the other, we
observe
a star six months apart, so that we are on opposite sides of the
sun for
each observation. Watch the star shift against background star
field, and
measure that shift.
Parallax Demo Animations (courtesy Erik Tollerud and James Davenport):
Define the parallax angle as half the observed shift:

Using trigonometry, we can solve for the distance. If we measure p in radians, we have:
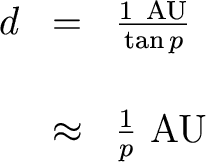
But we usually measure angles in arcseconds. Since 1 radian = 57.3o = 206265", we have
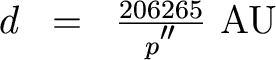
Okay, now comes the thinking part. Let's define a unit of measure called the parsec (pc) which is simply 1 pc = 206265 AU. Then we have
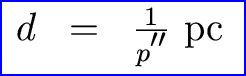
Stars are so distant that measuring parallax is
difficult. Satellite measurements:
| Hipparcos |
Gaia |
|
| Dates |
1989-1993 |
2014-2019 |
| Limiting magnitude |
~12 |
~ 20 |
| Parallax precision |
milliarcsec | 20 microarcsec (@ 15
mag) 200 microarcsec (@ 20 mag) |
| Distance |
< 1 kpc |
10 kpc |
| N(stars) |
~ 105 |
~ 2x107
(1% accuracy) ~ 2x108 (10% accuracy) |
| Velocities |
no |
yes -- radial and
space motions! |