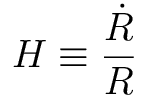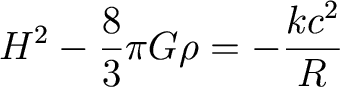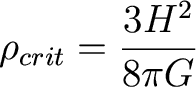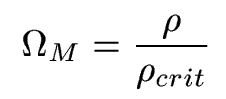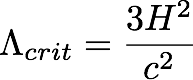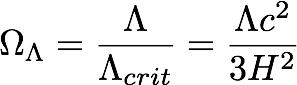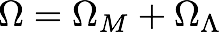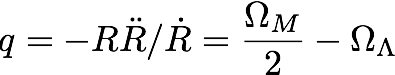Cosmological Parameters

---

1. The Hubble Parameter

The Hubble parameter is the normalized rate of expansion:

Note that the Hubble parameter is not a constant! The Hubble constant is the Hubble parameter measured today -- we denote its value by H₀. Current estimates are in the range of H₀ = 65-75 km/s/Mpc -- we will discuss these efforts in more detail later.

Also note you will often see the parameter h, particularly in distance-dependant quantities (for example, 75h^-1 Mpc). This is usually defined by h=H₀/100.

Look at the Friedmann equation:

Rewriting this using the Hubble parameter, and for now set Lambda=0:

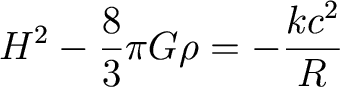
The Universe is flat if k=0, or if it has a critical density of

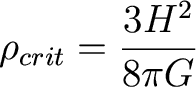
Remember, this is not the density that the universe actually is, its the density the universe would have to have if it was spatially flat by matter alone.

We define the matter density parameter to describe the actual density of the universe relative to this critical density:

So if Om=1, and there was no dark energy/lambda, the universe would be spatially flat. Best measurements for Om are about 0.25 - 0.35

 

 3. The "dark energy" density parameter

We can express a similar density parameter for lambda again by using the Friedmann equation and setting rho_m=0. This gives us a "critical lambda" that would flatten the universe:

And then we can define the dark energy density parameter analogously to the matter density parameter:




So if OL=1, and there was no matter, then the universe would be spatially flat. Best measurements for OL are about 0.65-0.75