The Robertson-Walker Metric

Let's go back to the cosmological principle: the universe is homogeneous and isotropic.

But waitaminnit! Everything is expanding away from us -- we are at the center of the Universe. How, then, can the universe be isotropic?
Answer: We aren't at the center of the Universe. In an expanding universe, everyone moves away from everyone else. There is no center.

We need a metric that reflects this -- it must be invariant under translations (homogeneous) and under rotations (isotropic). Only three possibilities exist, and they are all contained in the most general form of the spacetime metric (derived in 1934): the Robertson-Walker metric.

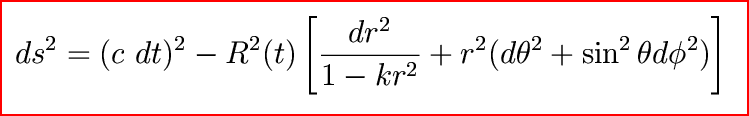
What is all this?

R(t): scale factor of the universe
k: curvature of spacetime

+1: positive curvature
0: flat space
-1: negative curvature

r, theta, phi: comoving coordinates

What do we mean by comoving coordinates?

Comoving coordinates are coordinates that move along with the overall expansion of the universe.
Imagine a distant galaxy. It is located at the coordinate (r,theta,phi). As long as no force acts on it, it will always be at that coordinate.
Its true distance does change, and is given by R(t) times the comoving distance (=Rr in a flat universe). But the change in the true distance is completely described by the change in the expansion factor R(t).
What could cause a galaxy to change its comoving coordinate?