Go back to Kepler's Third Law: ![]()
For a circular orbit
in general units, this becomes![]()
Orbital Period, P, is just ![]()
Substituting this P into Kepler's 3rd Law: 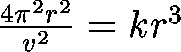
Multiply both sides by m and do some algebra, and we get
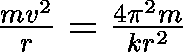
Now, do some thinking.
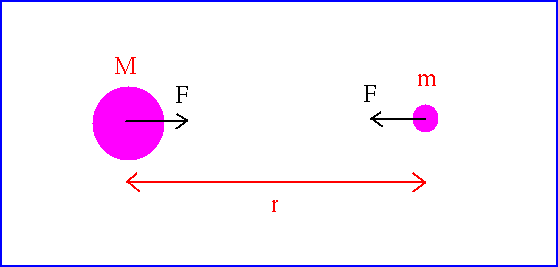
The left side is the centripetal
force that holds a planet in circular motion. This
must then be the gravitational force that holds the object in orbit. So,
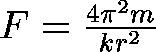
Do more thinking. Newton's Third Law says that the force the planet feels from the Sun must be the same as what the Sun feels from the planet. Gravitational force must be symmetric!
where G is called the "gravitational
constant" 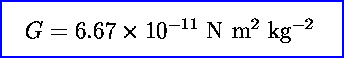
Finally, force is a vector quantity, so we must show this explicitly:
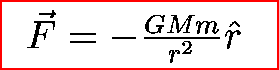
We derived this for objects on circular orbits, but it is true in general for any two objects: