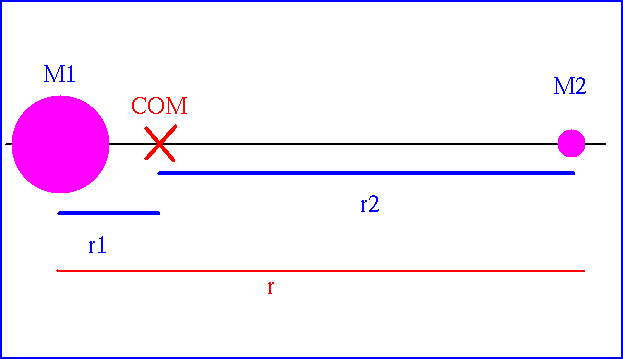
Actually, each star is on an orbit, but not around each other. They orbit the center of mass of the system.

Defining the center of mass:
M1r1 + M2r2 = (M1+M2)rcom
In other words, the distances r1 and r2 can change (ie., r can change), but the ratio r2/r1 is fixed. Also, the center of mass always lies on the line connecting the two stars.
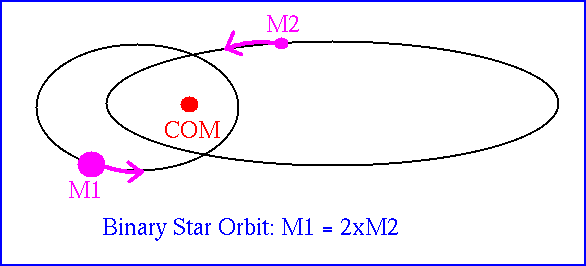
So here's that binary star orbit:
The gravity of the Sun makes the Earth (and planets)
move in an orbit. But gravity is symmetric, so the Sun must feel the
Earth's gravity.
Does the Sun also then move on an orbit?
So Kepler's First Law, revised:
Each planet moves on an elliptical orbit, with the center of mass at one focus.