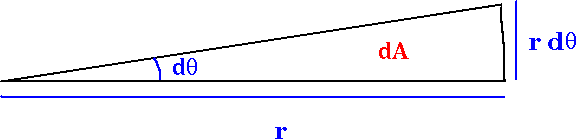
Consider a small wedge of the orbit traced out in time dt:

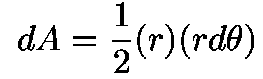
And the rate at which area is swept out on the orbit is
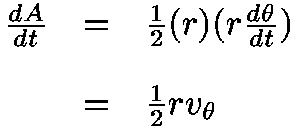
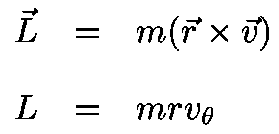
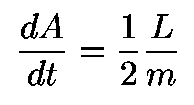
The rate at which a planet sweeps out area on its orbit is equal to one-half its angular momentum divided by its mass (the specific angular momentum). Angular momentum is conserved.