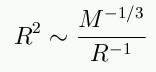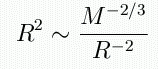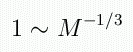But as we look at more and more massive white dwarfs,
they will have higher and higher densities. The electrons will be found
in higher and higher energy states, so their speed will approach the speed
of light. What happens if we do the same calculation with relativistic
degeneracy?
We get a strange result: for relativistic degeneracy,
you tend to a constant mass. But this can't really happen: if you
add more mass, you need faster-than-light electrons to support the WD,
which is impossible. If there is too much mass, the WD will collapse.
This means the "constant mass" is actually a maximum mass
that can be supported by degeneracy. This maximum mass is known as the
Chandraskhar
Limit, and is
Mch = 1.44 Msun
|
for relativistic degeneracy:
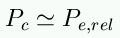
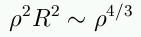
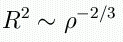
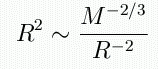
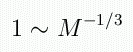
huh?
|