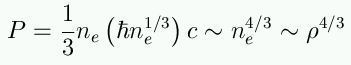White Dwarfs: Properties and Degeneracy
Sirius B: First white
dwarf discovered in 1862. Observed properties
-
M = 1 Msun
-
L = 0.03 Lsun
-
T = 27,000 K
From this, we can use Stefan-Boltzmann law to derive radius:
-
R=0.008 Rsun ~ Rearth
-
density ~ 3x106 gm/cm3
Not a normal star! We are seeing the central C/O core of
a dead low mass (M < 8 Ms un) star.
Let's estimate the central pressure inside a white dwarf:
Start with hydrostatic equilibrium:
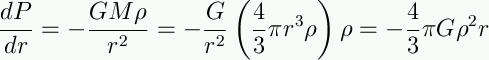
and integrate (assuming density is constant):
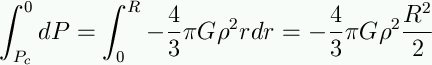
So we have an expression for the central pressure:
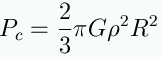
If we put in numbers for Sirius B, we get Pc
~ 4x1023 dynes/cm2 > 106 Pc,sun.
At these densities this high pressure is provided by electron
degeneracy.
Degeneracy
Remember two things from quantum mechanics:
-
The Pauli Exclusion Principle
from quantum mechanics: no two electrons can have the same quantum state
(i.e., energy level).
-
The Heisenberg Uncertainty Principle:
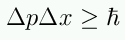
So how much momentum does each electron have? Each electron
must at least have a momentum equal to:
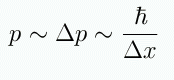
and how far apart are they? Higher density means the electrons
are more tightly packed. If the number density of electrons in the WD is
ne, then we have a average separation of
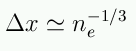
so then each particle's momentum is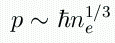
Now, what is the pressure? Think of particles bouncing
around in a box -- the pressure they exert on the walls is given by
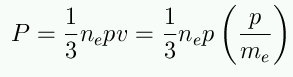
So, plugging in our expression for momentum we get
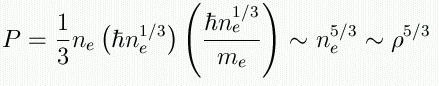
So for a degenerate gas, we have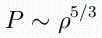
If the density is high enough, electrons keep getting
pushed to higher momentum, or higher velocities. But electrons can't move
faster than the speed of light -- their speed approaches, but does not
exceed, the speed of light. In this case, the pressure becomes
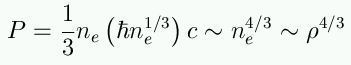
Or, for a relativistic degenrate
gas, we have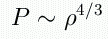
So what the heck does all this mean?
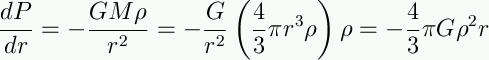
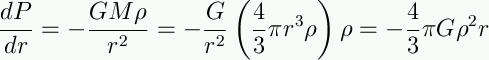
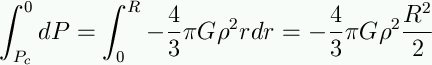
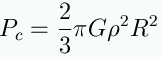
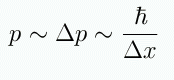
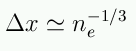
![]()
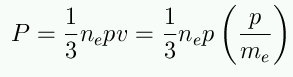
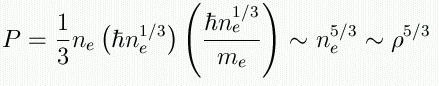
![]()