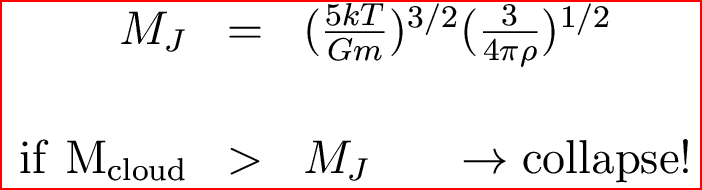
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
And the Jeans mass is given by:
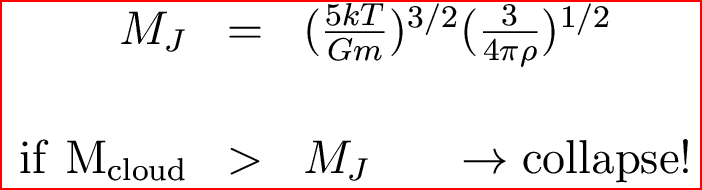
So plugging in numbers, we find that
How fast does this collapse happen? Let's do a "back of the envelope" calculation.
Consider a particle somewhere inside the cloud. What is the gravitational acceleration it feels pulling it inwards?
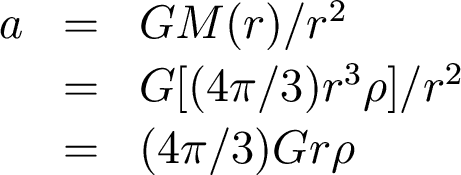
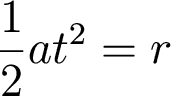
So, solving for t,
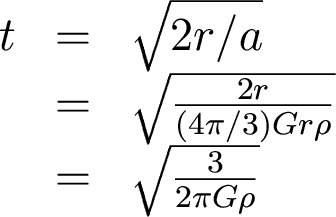
Now, since this is just a crude calculation, we can say that sqrt(3/2pi) = 0.7 = 1, so that we have an expression for the free fall time:
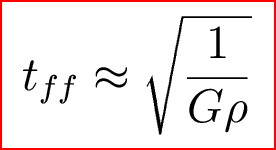
Note that the free-fall time depends only on density, not radius.
So how fast does the molecular cloud core collapse? Since it is mostly hydrogen,
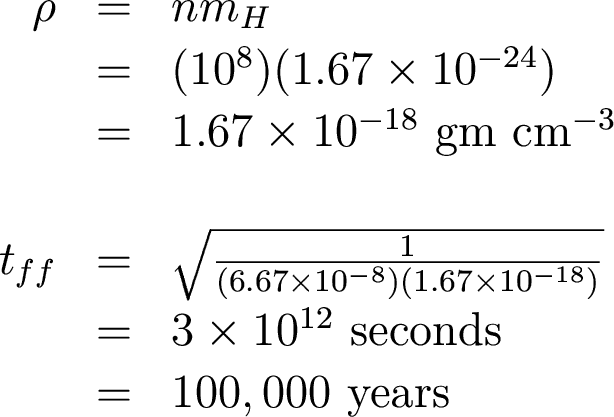
Fast! (by astronomical standards, anyway...)
As the cloud collapse, density rises. Since the collapse is isothermal, a rising density means the Jeans mass of the cloud is falling, so small pieces of the cloud start to collapse on their own. A rising density also means a declining free fall time, so these small dense clumps collapse faster than the overall cloud.
Instead of one giant cloud undergoing a monolithic collapse, the cloud fragments into small collapsing pieces.
So what stops this fragmentation?
Higher temperature means higher pressures (the ideal gas law), which halt the free collapse of the star. Since the cloud absorbs all the gravitational energy of collapse, it heats up, and it starts to act like a blackbody.
At what mass does this happen? We can balance
the rate of energy loss through gravitational collapse to the rate at which
the cloud radiates blackbody energy, and, solving for the mass (see pp
454-455), we find M ~ Msun. In other words, collapse
halts when the fragment masses reach star-like masses. Protostars!