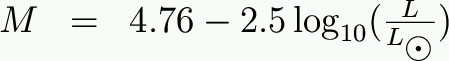So, not surprisingly, a star's apparent brightness depends on both its luminosity and its distance.
A star's observed magnitude is called its apparent magnitude (m), since is not a true measure of a fundamental property of the star.
Let's look at something which is a fundamental property of the star - its true brightness. We will define this as the brightness the star would have if it were 10 parsecs away from us. On the magnitude scale, we call this the star's absolute magnitude (M). How do we do this?
Start by defining f10 to be the flux you would receive from the star if it were 10 parsecs away. We can then relate distance (d) to absolute and apparent magnitude like this:
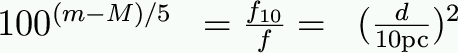
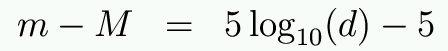
Often if we know what kind of star it is, we can estimate its luminosity (and, thus, M). We can then measure its apparent magnitude (m) and solve for distance. Since m-M is a measure of distance, it is called the distance modulus.
Question: what
is the
absolute magnitude of the Sun? Answer: M=4.76
(this, technically, is the bolometric
absolute magnitue of the Sun -- more on that later)
We can use this in a nifty way to relate absolute magnitude to solar luminosity. Remember our definition of magnitude: