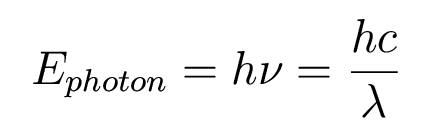
in 1860, Kirchhoff and Bunsen had been studying the spectral properties of matter and noted that some of the dark lines in the Sun were at the exact same wavelength as bright lines produced when sodium was heated up -- there must be sodium in the Sun.
Furthermore, they also published what are now known as Kirchhoff's Laws:
To understand this, we need two concepts: photons and atomic structure
Light can also be characterized by discrete particles called photons -- hence the wave-particle duality of light.
How much energy is contained in a single photon?
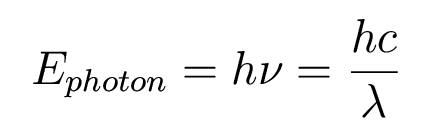
How was this discovered? Via the photoelectric effect:
It had been noticed that when light shines on a metal surface, electrons are ejected from the surface with a characteristic kinetic energy. If you increase the brightness of the light, you get more ejected electrons, but not at higher kinetic energies.Example: How much energy does a single blue (4000 Angstrom) photon have? Here is a quick tip to remember: hc=12400 eV A. So one 4000 A photon has 12400/4000=3.1 eV of energy.So even though you are bathing the metal in more energy, the electrons coming off have the same maximum energy.
Einstein explained this by suggesting light was made up of discrete particles -- photons -- that had a discrete amount of energy. More photons could eject more electrons, but not at higher speeds. This is what Einstein won the 1921 Nobel Prize for, not his work on special and general relativity.
Consider the hydrogen atom - 1 electron in orbit around 1 proton. Simple!
The allowed energy levels in the hydrogen atom are given byThink of this visually, in terms of orbits (this is not really correct, but it is a useful analogy...)
- If the electron is in the n=1 state, the energy is -13.6 eV and it is called the ground state of the atom
- If the electron is in the n=2 state, the energy is -3.4 eV and it is called the first excited state of the atom
Now, what would happen if an electron moved from one level to another? The energy of the atom would change! How could this happen?
In the hydrogen atom, transitions to/from the n=2 level involve energies which correspond to optical photons. These transitions were the first discovered, and are called the Balmer series.
- If an electron moves up to a higher state, the atom must have gained energy, by absorbing a photon. But it can't absorb any old photon, it must absorb one with exactly the right energy. So if you want to move from n=1 to n=2, the energy difference is 13.6 eV - 3.4 eV = 10.2 eV. What photon has exactly that energy? One with a wavelength of 1216 A.
- If an electron moves down from a higher state, the atom loses energy, so it must emit a photon. But again, only a photon which carries away the exact amount of energy difference. If the electron was going from n=2 to n=1, it would emit a photon of 1216 A.
Transition Name Wavelength n=3 to/from n=2 Halpha 6563 A n=4 to/from n=2 Hbeta 4861 A n=5 to/from n=2 Hgamma 4340 A n=6 to/from n=2 Hdelta 4102 A The first four Balmer lines Other series include
Here is an energy level diagram for the hydrogen atom:
- transitions to/from the ground state (n=1): The Lyman series
- transitions to/from the n=3 state: The Paschen series
Enough nonsense -- show us a real spectrum! Okay, here is a spectrum of a hot, blue star called an A star.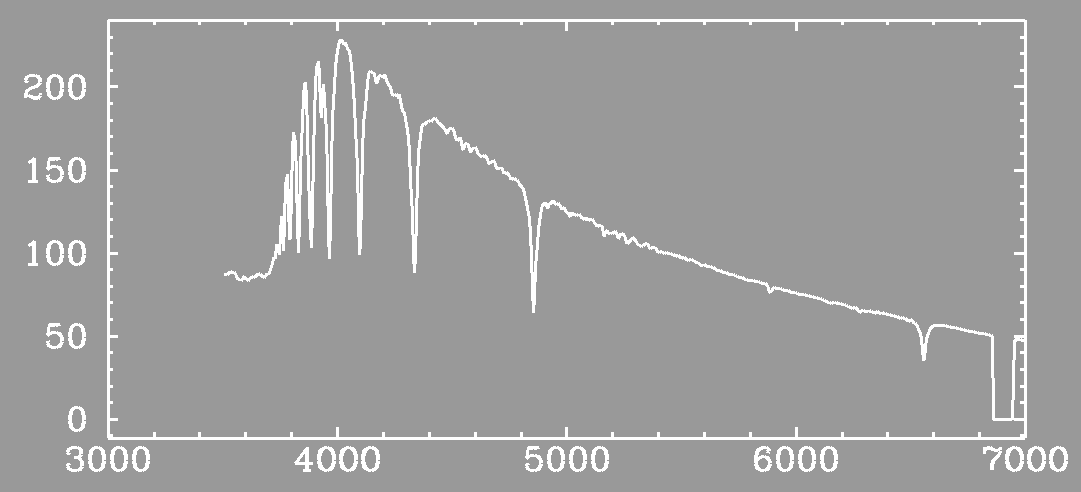
(courtesy Diamond Dave Silva)Wow! Look at those Balmer lines!