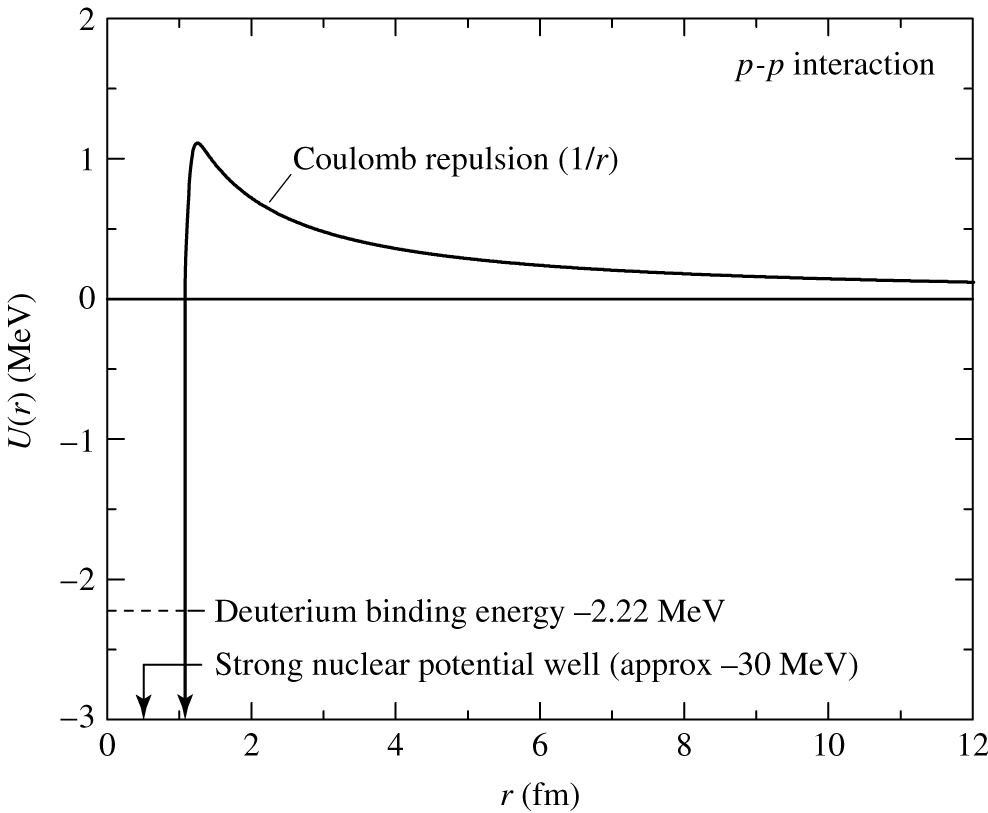
Protons have positive charge. Like charges repel
-- the
electromagnetic force.
We need to overcome this repulsion to have
the
nuclei fuse.

How do we do this? Energetic
nuclei! How do
we make energetic
nuclei?
Particles at a given temperature will have a distribution
of speeds (and therefore a distribution in
energies):
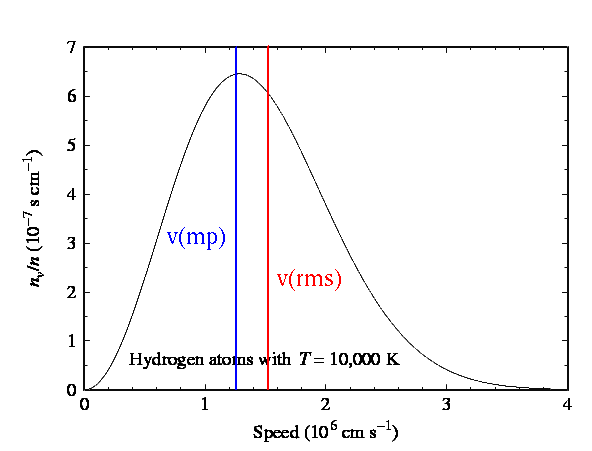
And, in this distribution, particles have a most probable velocity and an average velocity:
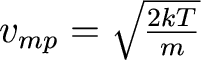
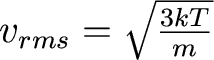
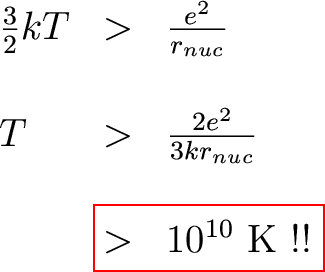
Well, things aren't that bad. There is a high
energy tail
to the distribution. But this alone isn't enough. We need to
look to quantum
mechanics.
The Heisenberg Uncertainty Principle: It is not possible to know both a particle's momentum and position to unlimited accuracy. In other words,
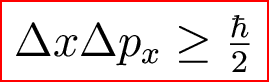
So combining the high energy tail of the M-B distribution and the possibility of QM tunneling (which rises as energy rises), we get the Gamov peak:
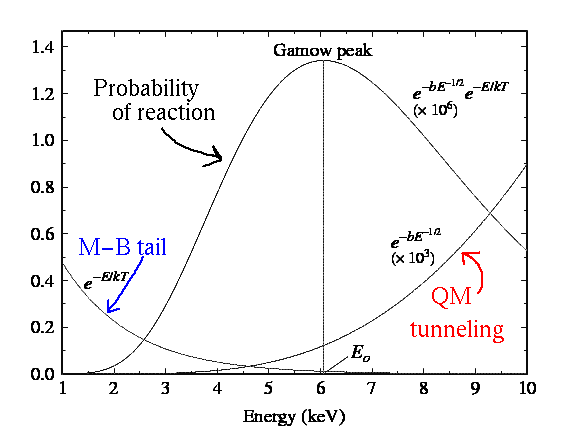
 Voila!
Nuclear
Reactions!
Voila!
Nuclear
Reactions!