Getting out of the Photosphere

The energy reaches the upper levels and where the opacity drops and it can move again the last step out via radiative transfer.

Let's review the concepts behind absorption (remember our discussion from planetary atmospheres...).

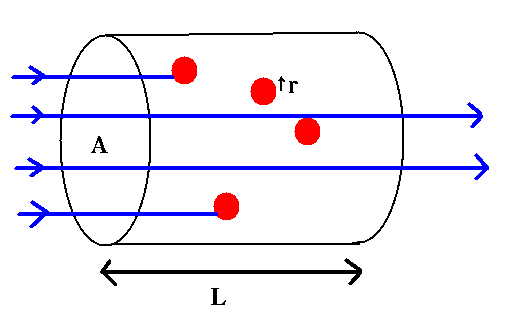
Look at light rays passing through a cylinder of absorbers:

A: area of the cylinder's end
L: length of the cylinder
r: size of absorbers
n: number density of absorbers

We can define a cross-section for absorbing as

(This is a geometric definition. For atomic/nuclear processes it is more realistically a probabalistic definition.)

Then,

and

As long as the absorbers don't shadow each other, the fractional area blocked is

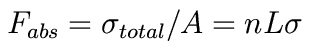
Then the fraction of light blocked is

We refer to this as the optical depth:

If the optical depth is large, we say the region is optically thick -- light is readily absorbed. If the optical depth is small, the region is optically thin, and light passes through easily.

Often, we will also talk about the column density (aka surface density) of material. Imagine squashing that cylinder along its axis. Then the number of absorbers per unit surface area is given by the column density:

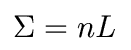
Note that the absorbing cross section of atoms varies strongly with wavelength, so that the optical depth varies strongly with wavelength.

Optically thick regions

We said that the optical depth was the fraction of the light absorbed, as long as the absorbers don't shadow one another. If there are lots of absorbers (ie region is very optically thick), this definition breaks down. We need to do things a bit more carefully here.

Think of an optically thick layer as a bunch of optically thin layers all stacked together:

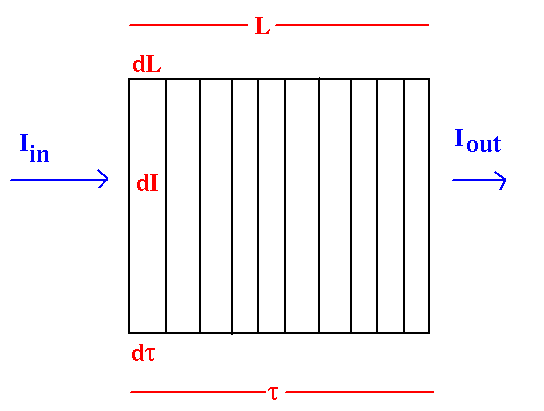
In each optically thin layer, the change in radiation intensity, dI, is simply equal to the intensity coming in times the optical depth of that layer:

So we have the following differential equation:

Let's integrate this:

I goes from I_in to I_out, while tau goes from 0 to tau:

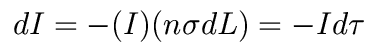
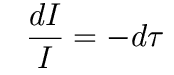
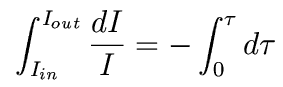
This integrates to

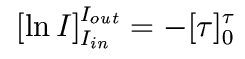
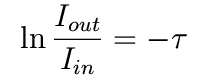
In other words,

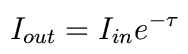
So as optical depth gets large, the amount of light drops exponentially.

If we go back to the optically thin case,

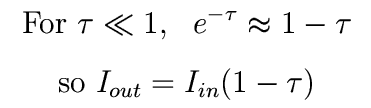
we see again that tau is the fraction absorbed, so the expression holds for any optical depth.

Question: How large must the optical depth be in order to absorb

1% of the photons?
10% of the photons?
50% of the photons?
99% of the photons?

We say that we see (more or less) into an object down to a physical depth where the optical depth becomes unity. So we see further into a diffuse medium than into a dense one...

The photosphere: the region in the sun where the optical depth becomes ~ 1. This means photons can move easily outward, carrying energy away: sunlight!