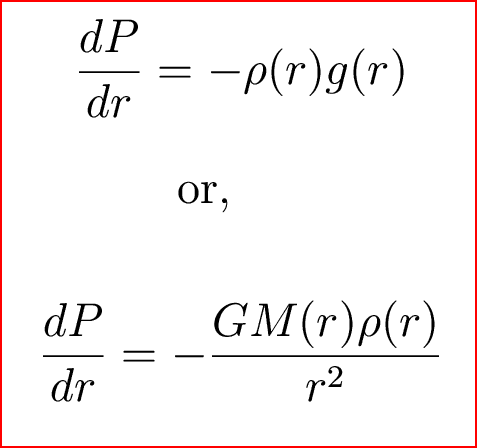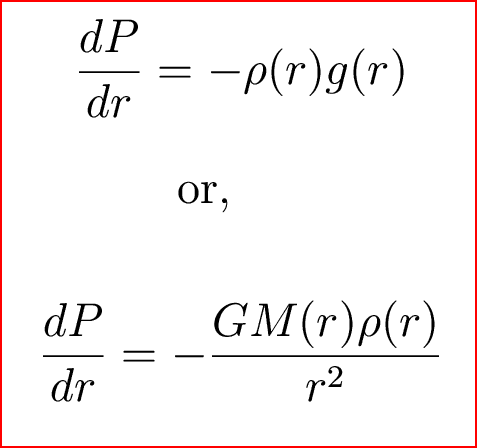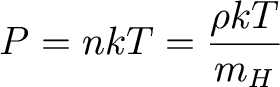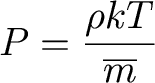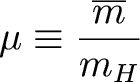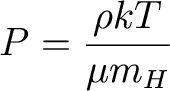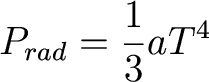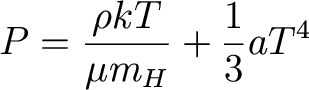Stellar Interiors
Remember what controls the interior of a star:
- hydrostatic equilibrium
(pressure gradient of the star balances gravitational collapse)
- equation of state
(relates density, temperature, and pressure)
- energy production
(nuclear reactions)
- energy transport
(radiative, convective)
So far we have talked about how these things work
inside the Sun; now we generalize and look at how they work in
different stars.
Hydrostatic Equilibrium
Remember the equation of
hydrostatic equilibrium:
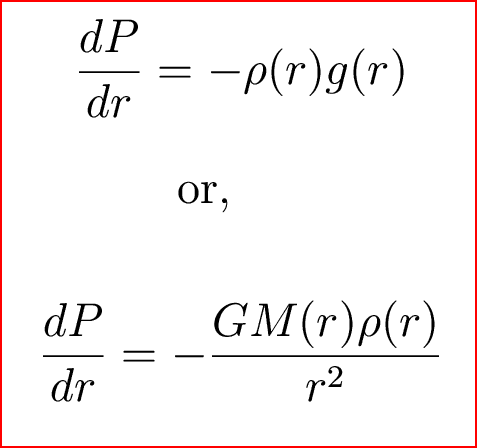 where P is
pressure, rho is density, M is mass, g
is the gravitational acceleration, G
is the gravitational constant, and r
is the radial distance from the center of the star.
where P is
pressure, rho is density, M is mass, g
is the gravitational acceleration, G
is the gravitational constant, and r
is the radial distance from the center of the star.
Equation of State
For stars on the main sequence, the equation of state
is that of an ideal gas. We have
typically written the ideal gas law like this, assuming hydrogen gas:
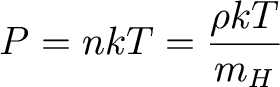 But we will not assume a pure hydrogen gas any longer!
The gas has some chemical composition, so the equation of state becomes
But we will not assume a pure hydrogen gas any longer!
The gas has some chemical composition, so the equation of state becomes
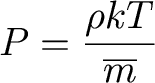 Where mbar is the average mass of the particles (atoms,
ions, or molecules) in the gas.
Where mbar is the average mass of the particles (atoms,
ions, or molecules) in the gas.
Let's introduce a quantity called the mean molecular weight (mu), defined as
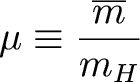 which then lets us write the equation of state as
which then lets us write the equation of state as
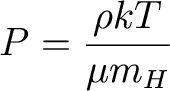
Question: What is
the mean molecular weight of
- a pure hydrogen gas?
- a pure helium gas?
- an ionized pure hydrogen gas?
- an ionized pure helium gas?
Okay, what is the mean molecular weight of the gas
inside the sun?
The chemical composition of the Sun
We characterize the composition of the Sun (and other
stars) in terms of the mass fraction of different elements:
- X=(total
mass of hydrogen)/(total mass of
star)
- Y=(total
mass of helium)/(total mass of
star)
- Z=(total
mass of everything else)/(total
mass of star)
Z is called the metallicity
of the star, and X+Y+Z=1
Chemical Composition of the Sun's
Atmosphere
|
Element
|
Atomic Number
|
Log(Abundance)
|
|
Hydrogen
|
1
|
12.00
|
|
Helium
|
2
|
10.99
|
|
Oxygen
|
8
|
8.93
|
|
Carbon
|
6
|
8.60
|
|
Neon
|
10
|
8.09
|
|
Nitrogen
|
7
|
8.00
|
|
Iron
|
26
|
7.67
|
|
Magnesium
|
12
|
7.58
|
|
Silicon
|
14
|
7.55
|
|
Sulfur
|
16
|
7.21
|
Adding this all up, for the Sun,
X=0.7
Y=0.28 Z=0.02
From X, Y, and Z, you can
calculate the mean molecular weight. For the Sun, we have
- mu=1.30 (if the gas is not
ionized)
- mu=0.62 (if it is ionized)
So what? Big deal.
Well, what is happening
inside the center of the sun? How is this changing mu? How does this
change the central pressure under the ideal gas law?
Radiation Pressure
Atoms and ions aren't the only thing running around in
the center of stars. There are also plenty of photons, and they exert a
pressure as well.
Remember that photons
carry momentum
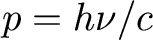 So that they can give momentum to particles which
absorb them. Integrating over the Planck function, we can get an
expression for the pressure:
So that they can give momentum to particles which
absorb them. Integrating over the Planck function, we can get an
expression for the pressure:
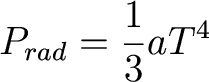
So that our total equation of state is
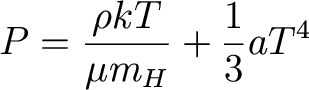
For the sun, radiation pressure is negligible. For
other stars it is not (which kinds of stars?).