A Different Approach

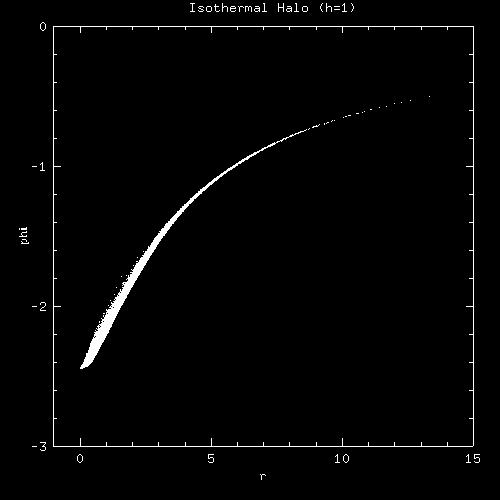
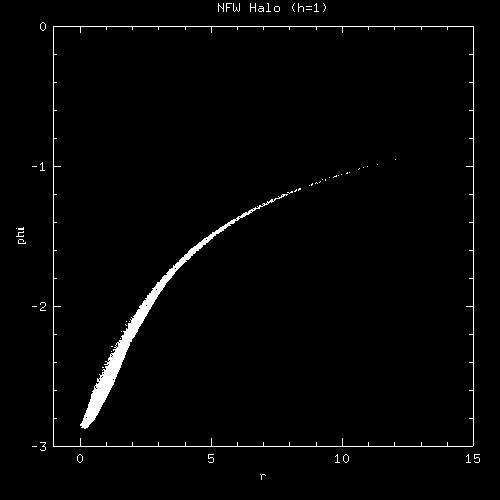
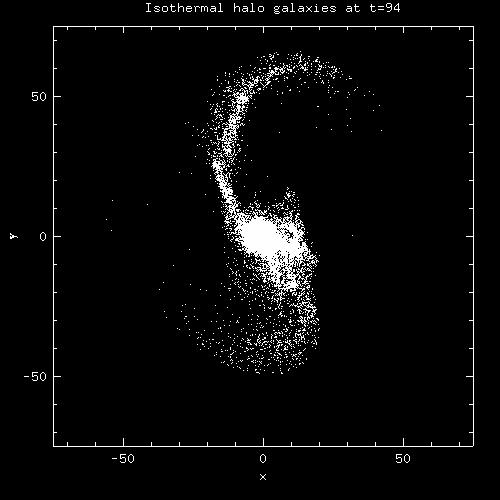
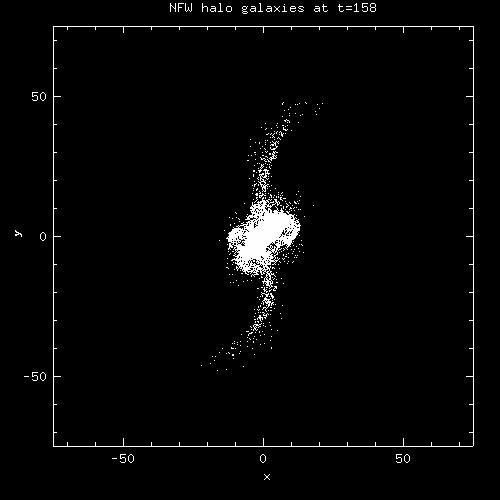
Notice that each time we changed how stars were distributed in the galaxy's potential, the mass distribution in the tails changed. This means the ability to make tails is highly dependent on the galaxy potential and how stars are distributed in it. If we can create a criteria for whether or not a galaxy can create tails in an interaction, based on the potential, perhaps we can constrain truncation radii in a more general way.

Tails are made when stars in the galaxy are given the orbital energy that the galaxies lose as they spiral together. So, we are going to postulate that there is a critical amount of energy that the tail stars need to have to be a part of the tail.

By using the potential of an undisturbed galaxy:	(Bush & Mihos)	(Bush & Mihos)
And the energy of the stars in the galaxy after the first pass:	(Bush & Mihos)	(Bush & Mihos)
And finally the energy the stars have at the time we were evaluating tails earlier:	(Bush & Mihos)	(Bush & Mihos)

We can derive this critical energy.

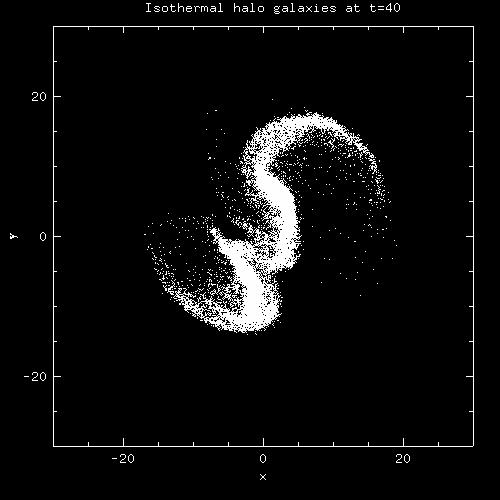
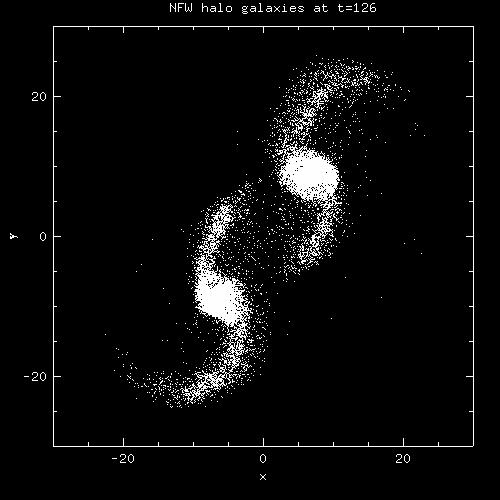
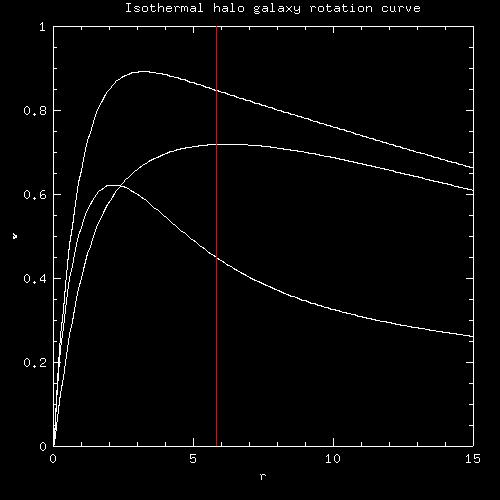
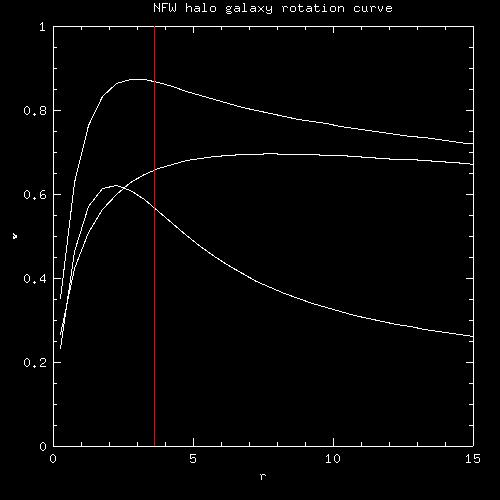
The following graph shows which particles in the final simulation could make it into tails at a given critical energy. So if the tail is selected in a plot, that is the critical energy that defines the tail.
Isothermal halo galaxies
NFW halo galaxies

We derived which radius this critical potential corresponds to in the initial galaxy, and plotted this on the rotation curve of the initial galaxy:

(Bush & Mihos)

(Bush & Mihos)

It looks like this radius could correlate with the maximum of the overall rotation curve but a larger sample of models would be needed to confirm this result.